拓扑学上的紧致性怎样理解？有何运用？

谢邀：紧性是空间最重要的性质之一，所谓的理解是建立在应用基础上的，离开这些例子，光靠解释是没用的。反过来，如果你都知道一些例子，你自己大概也能归纳出来。本质上紧性是允许我们像处理有限维空间那样处理一些无限维空间。 特别的的，连续函数在一般的拓扑空间上的有界闭集上不一定有界，但是在紧集上确是可以达到最大最小值。我在下面的回答中列出了大量有限维和无限维上“函数”的区分：

能不能把泛函简单地理解为函数？ - dhchen 的回答 - 知乎

就算是一个拓扑里面紧性也可以定义两种：紧和列紧。为了讨论方便，我只谈列紧性。对于一个（列）紧集， 必然有子列 收敛到某个点 。紧性的用处很大，下面我举两个例子：

第一，利用紧性得到某个极小值，然后这个极小值可以推出所要的数学结果。比如，它可以证明代数基本定理：

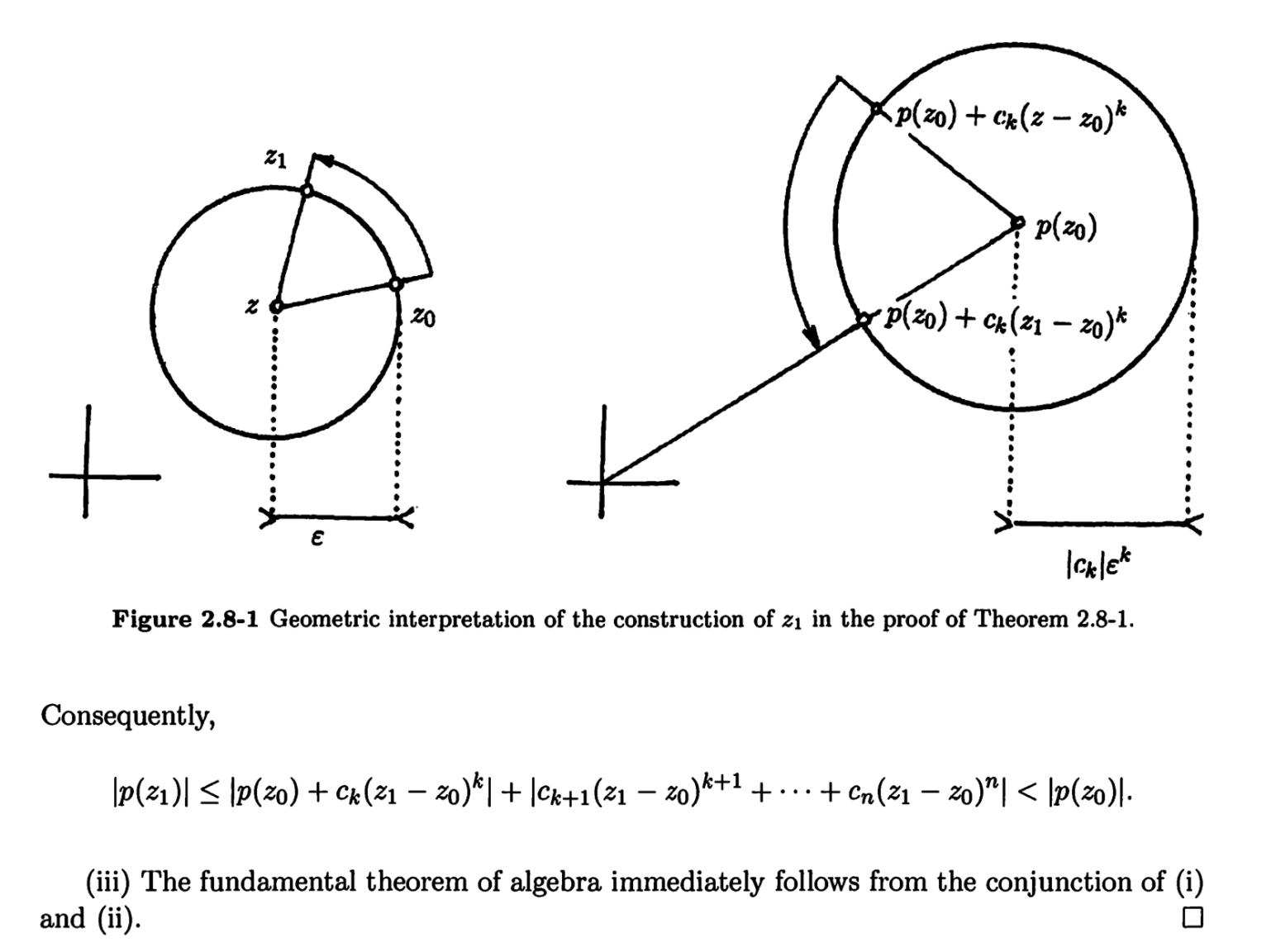
第二，偏微分方程上证明解存在性的一个思路是这样的：为了解 ,我们首先找出容易解的一列方程 使得 ,算出他们的解 ,然后证明它们在一个紧集合内，自然你可以找出一个极限 ,于是我们有 。下面我举一个例子。

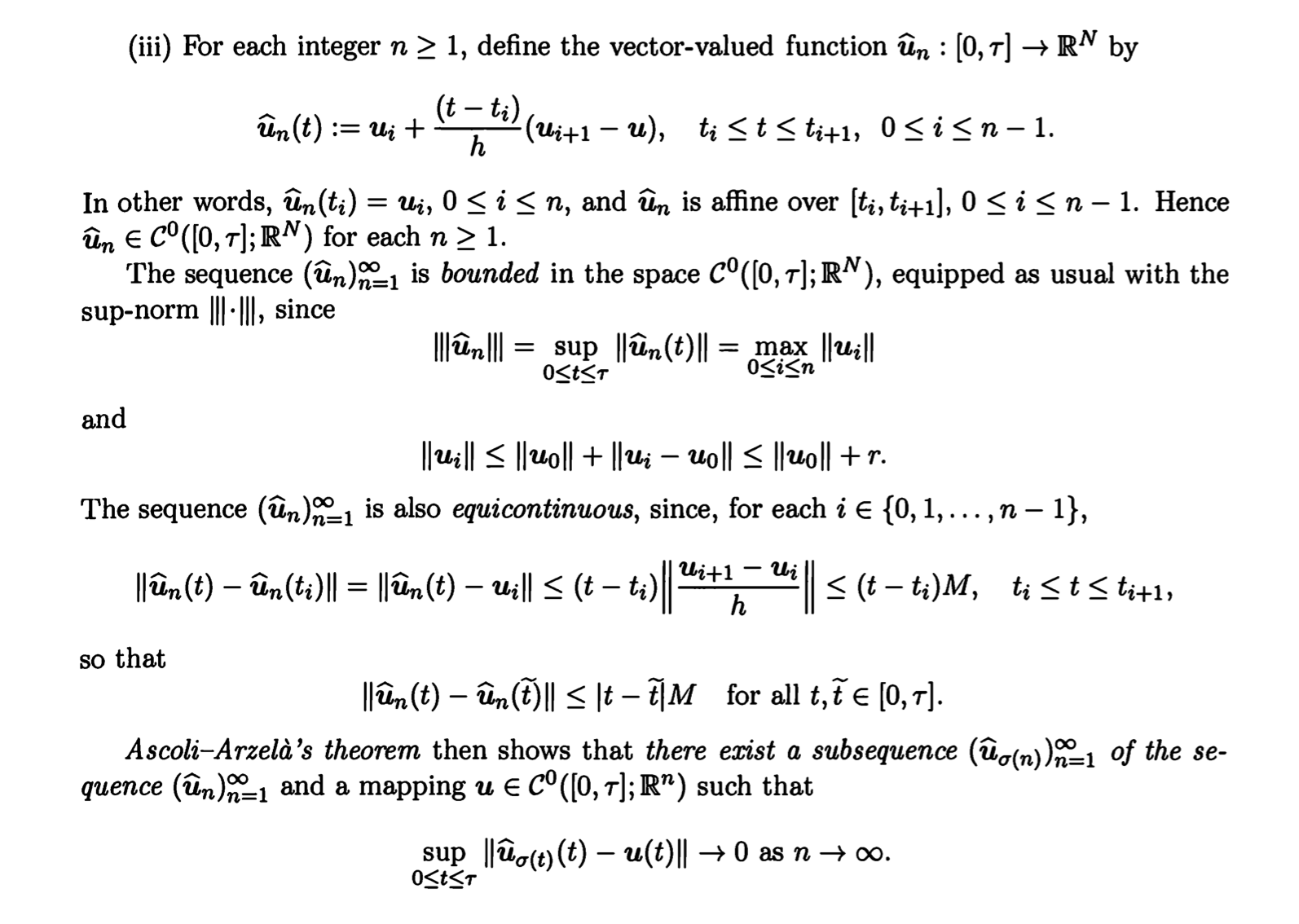
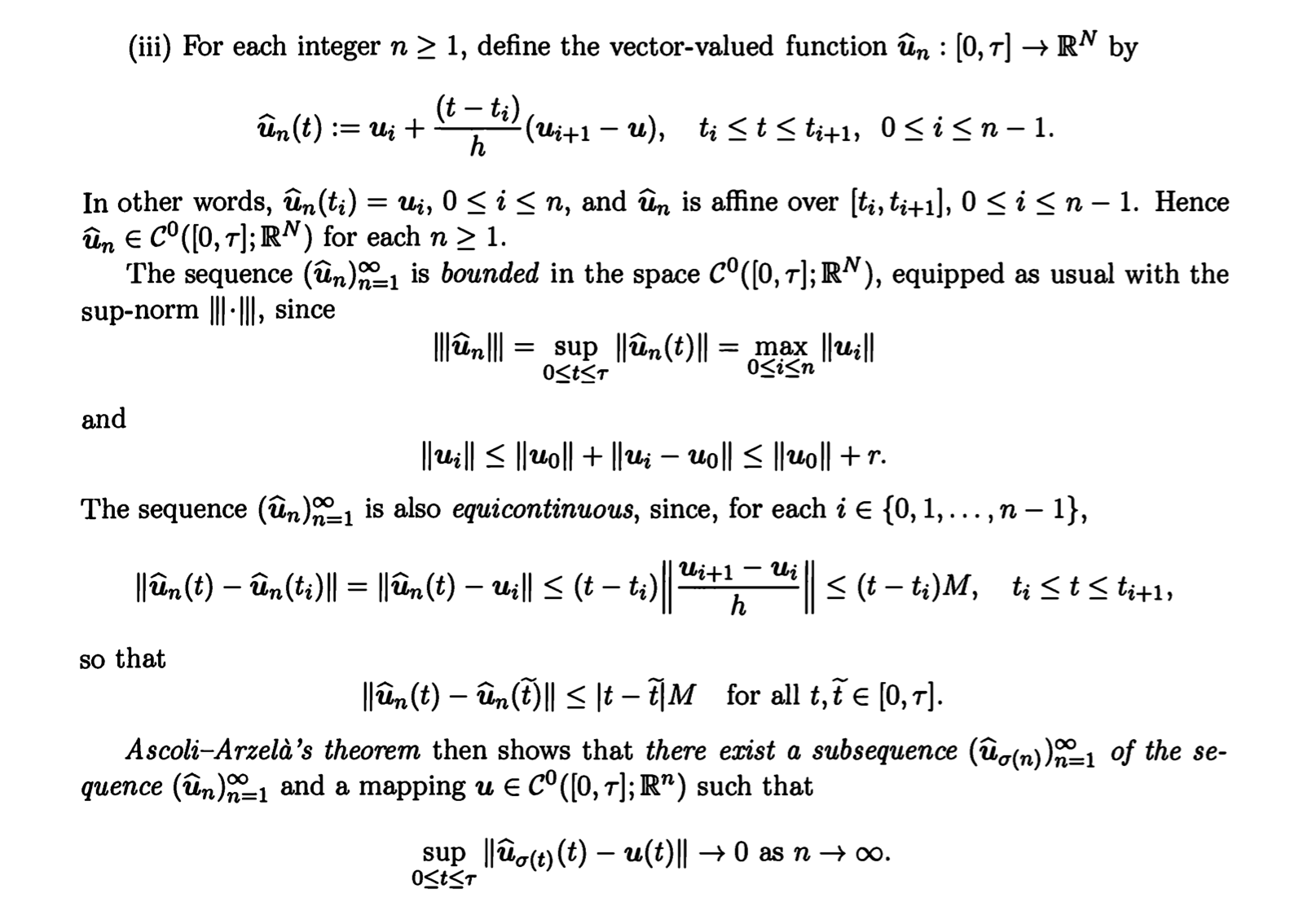
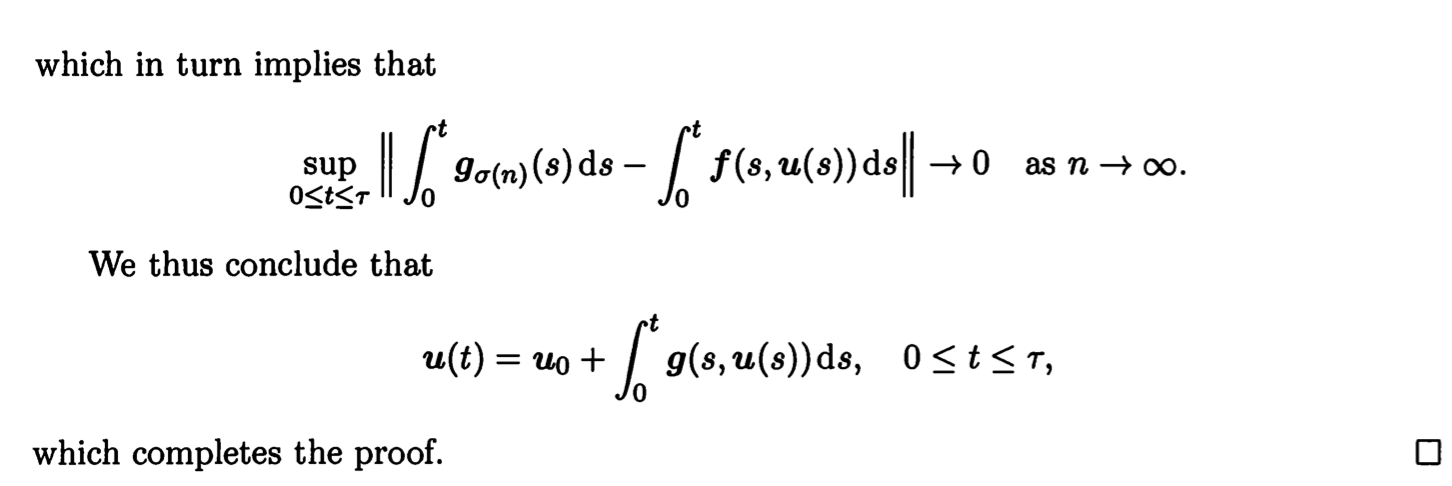
第三，很多偏微分方程等价于某个拓扑空间上泛函的极小值问题：

研究增这类泛函极小值的方法：变分法的direct method里面第一条就是利用紧性来证明极小值的存在性。举个例子：带有第一类边界条件的

弱解的存在性等价于

在希尔伯特空间 上泛函极小值。level set

在某个弱拓扑下是列紧的，从而基于这个泛函的弱列下半连续性可以推导出极小值是存在的。

对于初学者紧性不是很直观的东西，毕竟历史上在对实数系的研究中它是后来才被发现占据如此根本性的地位的。不过如果要在形式上理解是很容易的。

紧性在证明中常常被用来从空间每一点得到的某种开集类中，直接得到一个有限开覆盖，比如有限交性质的证明。这类技巧多用几次就知道紧性这个东西有多好了。

熟悉了之后很容易能够粗略地谈紧性到底是什么，比如反映了局部性质可以反映在整体上之类的，不过这种描述一般只会给初学者带来困惑，所以还是多看例子比较重要。

谢邀

我就先说一句吧

紧性是需要关于有限的或者有限才能得到的性质的首先应该想到的东西

数学分析中讲到：R中闭区间[a,b]上连续函数具有一些好的性质，比如有界、能取到最值、介值定理、连续等价于一致连续等。

那么这些结论是怎么推广到泛函分析和拓扑学的呢？

1. 先推广到n维欧氏空间R^n，(注：由于任何有限维n维空间都与R^n代数同构、拓扑同胚，也相当于推广到有限维空间)

空间R^n上的连续函数(叫泛函)，也要具有那些好的性质，有界、最值可达、连续就一致连续等，需要把原来的闭区间[a,b]换成“有界+闭”集，就也可以保证。

2. 进一步推广到无穷维Banach空间(完备赋范线性空间)，或更一般的距离空间

也想保证某类集合上的连续映射具有上述好的性质，这时候，因为空间的条件减弱了，对集合的要求只有“有界+闭"就不够了，就得需要更强一点的条件，那就是列紧集(在距离空间与紧是等价的)

其实，列紧的定义就是任意无穷点列都有收敛子列，而这也是保证连续映射具有那些好的性质所需要的根本条件。为什么有限维空间，"有界+闭"就能够用，也是因为它已经能保证任意无穷点列都有收敛子列。

3. 进一步，列紧在拓扑空间不能这么说的，因为拓扑空间里有的结构是拓扑结构，开集啊邻域啊这些。好在，距离空间中自列紧(列紧+闭)，也有另一种等价描述：任意的开覆盖都存在子覆盖。这种描述才是紧集根本的，拓扑空间也适用，于是就推广到拓扑空间中的紧集概念。

紧致意味着一定有有限覆盖。琢磨这有限子集族就足够产生丰富结果，比如Cech 复形。

也就是说，紧致保证了拓扑问题可以变成有限指标的组合数学游戏。